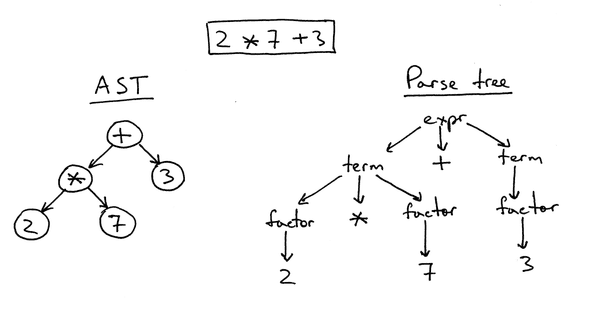
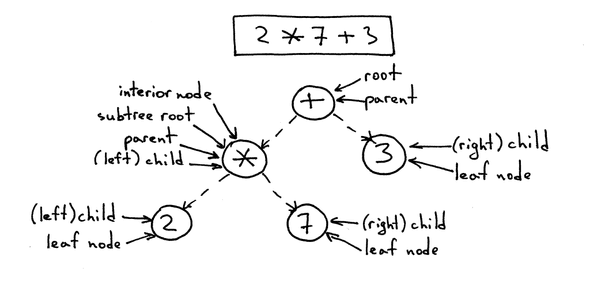
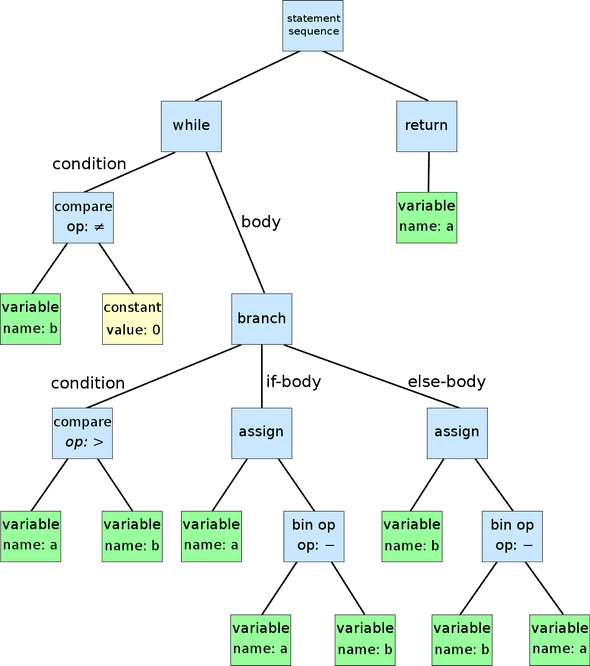
Write a "mini-compiler" in TypeScript

Trong ngôn ngữ lập trình, chúng ta thường quen với các khái niệm statement và expression. Các statements sẽ thực hiện một hành động/phép tính, còn expressions khi được compiler evaluate (thẩm định) sẽ trả về một giá trị nào đó - trong các kiểu sau:

String
Number
Boolean (true hoặc false)
Object

Chi tiết hơn, một statement là một tập lệnh có thể được execute (thực thi), có thể nói tới như:

while
for loop
Phép gán biến
Khai báo biến
if else

Các expressions cần được compiler evaluated để tạo ra giá trị:

1 + 4

Expression ở trên khi được evaluated thì sẽ trả về giá trị là 5:

2 < 4

Còn cái expression trên thì sẽ trả về giá trị true.

Vậy tóm lại, một expression là một sự kết hợp giữa nhiều giá trị, biến (variable), phép tính (operator) và các lệnh gọi hàm (function).

Statement sử dụng giá trị được trả về bởi expressions để thực thi một hành động hoặc để biết về một hành động cụ thể cần được thực thi trong trường hợp đó (if / else).

Hãy xem qua cấu trúc cơ bản của một if statement:

if (cond expression) {
    // ...
    // body
}

Phần body của if statement sẽ được thực thi nếu cond expression giữa hai dấu ngoặc kép trả về giá trị true.

Một giá trị nằm riêng sẽ là một expression:

1
23
445
'hello'
true

Chúng được gọi là primary expressions. Nếu được evaluated, chúng sẽ trả về giá trị của chính nó. Expressions xuất hiện bên phải của một phép gán.

b = 78 * 56
a = 98 * 67 + 454 - 909

Như bên trên là các phép gán, các phép gán là statements bởi vì chúng không trả về giá trị. Chạy các phép gán trên trong compiler sẽ trả về như này:

>> b = 78 * 56
>> a = 98 * 67 + 454 - 909

-> Không có gì cả, nhưng khi chúng ta in ra biến a và b:

>> b = 78 * 56
>> a = 98 * 67 + 454 - 909
>> b
4368
>> a
6111

Giá trị của các biến này được in ra bởi vì chúng là các primary expressions. Các phép gán ở trên không được in ra gì bởi vì chúng là một statement và chúng chỉ được thực thi mà không được evaluated.

Một số thứ được thực thi để thực ~~~~hiện một hành động nào đó nhưng một số thứ khác lại được evaluated để trả về một câu trả lời (một giá trị).

Bây giờ, chúng ta đã có thể hiểu về expression, sau đây chúng ta sẽ thử viết một evaluator program bằng TypeScipt - evaluator này sẽ parse và evaluate các expressions được truyền vào.

Để dễ hình dung hơn, evaluator program mà chúng ta muốn viết sẽ có output như này:

const str = `
    5+9
    3 + 3
    2 + 2 + 2;
    22*9 - 2*90
    66>=90
    90>1
    88==7
    3*250*360
    (45*89)+90
    4-5+6
    4-(5+6)
`
const asts = useParser().parse(str)
evaluate(asts)

Và sau khi chạy các lệnh trên, kết quả trả về như sau:

$ node .
======================== RESULTS ========================
14
6
6
-3762
false
true
false
270000
4095
-7
-7

Bắt đầu…

Trước tiên, ta cần khởi tạo một project Node.js với npm:

$ mkdir expr_parser
$ cd expr_parser
$ npm init -y

Cài đặt TypeScript compiler:

$ npm install typescript -g

Scanning và Tokenizing

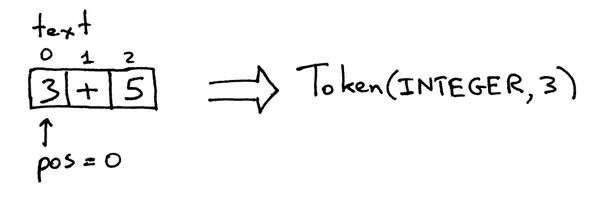
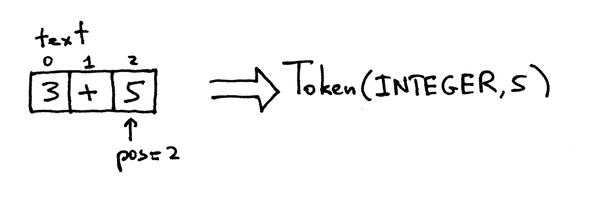
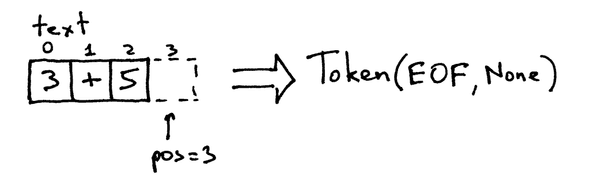
Điều đầu tiên cần làm là tokenize các expressions. Tokenizing nghĩa là chia nhỏ expression ra thành nhiều phần nhỏ tách biệt.

Ví dụ:

2 + 45 - 90

Expression trên có thể được chia tách ra thành các tokens:

[
    {
        value: '2',
        type: Number
    },
    {
        value: '+',
        type: AddOp
    },
    {
        value: '45',
        type: Number
    },
    {
        value: '-',
        type: SubOp
    },
    {
        value: '90',
        type: Number
    }
]

Về chi tiết, tokenizing sẽ chia nhỏ các thành phần ra để chia sẻ với Parser về mỗi đơn vị thể hiện cái gì. Trong expression 2 + 45 - 90, ta có 5 đơn vị hoặc tokens:

+---+ +---+ +----+ +---+ +----+
| 2 | | + | | 45 | | - | | 90 |
+---+ +---+ +----+ +---+ +----+

Trong mảng ở trên, mỗi token có một đặc tính value và type. Phần tử đầu tiên trong mảng là một Number và phần từ thứ hai là một Operator +, kiểu là AddOp…

Nếu chúng ta có một expression như này:

90 * (78 - 65) / 90

Sau khi tokenizing:

+----+ +---+ +---+ +----+ +---+ +----+ +---+ +---+ +----+
| 90 | | * | | ( | | 78 | | - | | 65 | | ) | | / | | 90 |
+----+ +---+ +---+ +----+ +---+ +----+ +---+ +---+ +----+

Thể hiện trên mảng sẽ là:

[
    {
        value: '90',
        type: Number
    },
    {
        value: '*',
        type: MulOp
    },
    {
        value: '(',
        type: LParen
    },
    {
        value: '78',
        type: Number
    },
    {
        value: '-',
        type: SubOp
    },
    {
        value: '65',
        type: Number
    },
    {
        value: ')',
        type: RParen
    },
    {
        value: '/',
        type: DivOp
    },
    {
        value: '90',
        type: Number
    }
]

Những token này sẽ cho ta biết về mỗi đơn vị của expression đại diện cho cái gì, là Number, hay Division Operator, hay là Subtraction Operator, …

Giờ thì hãy tạo một tokenize function, function này sẽ nhận vào 1 tham số: string mà ta muốn tokenize, và trả về một mảng các tokens.

Khi parse trên token thì tokenize function cũng sẽ phải validate các trường hợp expression được coi là không hợp lệ, ví dụ ta có một expression là 34+4.

3 sẽ là một valid expression, 34 cũng thế, 34+ thì không.

import { isNum, isOp } from './utils' // Check if the string is a number / is an operator

type TokenType = 'NUM' | 'LPAREN' | 'RPAREN' | 'OP' | 'EOL' | 'EOF'

interface Token {
  type: TokenType,
  value?: string
}

function tokenize(str: string): Token[] {
  const tokens: Token[] = []

  str = str.trim()
  let s = ''
  for (let index = 0; index < str.length; index++) {
    s += str[index]
    const peek = str[index + 1]

    if (isNum(s.trim()) && !isNum(peek)) {
      tokens.push({
        type: 'NUM',
        value: s.trim()
      })
      s = ''
    }

    if (s.trim() == '(' || s.trim() == ')') {
      s.trim() == '(' ?
        tokens.push({ type: 'LPAREN' }) :
        tokens.push({ type: 'RPAREN' })
      s = ''
    }

    if (isOp(s.trim()) && !isOp(peek)) {
      tokens.push({ type: 'OP', value: s.trim() })
      s = ''
    }

    if (s == ';' || s == '\n') {
      tokens.push({ type: 'EOL' })
      s = ''
    }

    if (index == (str.length - 1)) {
      tokens.push({ type: 'EOF' })
      s = ''
    }
  }

  return tokens
}

Trong hàm tokenize đầu tiên ta trim string để xóa các whitespaces dư thừa, sau đó ta lặp qua các phần tử trong string bằng for loop.

Đầu tiên, chúng ta sẽ chỉ sét các token sau đây:

Numbers
Operators
Left Paren (dấu ngoặc trái) ( và Right Paren (dấu ngoặc phải) )

Ta nối mỗi giá trị của for loop index hiện tại vào một biến s, peak là một con biến để lưu giá trị tại for loop index + 1. Khi lặp nếu cả s và peak đều là number thì ta sẽ chưa thể tạo 1 tokens number do chuỗi con của number này chưa kết thúc, ngược lại thì ta sẽ tạo ra 1 token type là Num và đưa vào mảng tokens.

Ví dụ đi:

345+90

Vòng lặp đầu tiên, biến s sẽ có giá trị là 3, lúc này vẫn chưa tạo được token vì peek có giá trị là 4, vẫn là một number, tương tự cho vòng lặp tiếp theo, s = 34 và peek = 5, vẫn chưa được. Vòng lặp thứ ba, s = 345 và sẽ tạo được Number Token vì peek lúc này là +, không phải number, push number 345 vào mảng tokens, mảng tokens lúc này:

[
    {
        type: 'NUM',
        value: '345'
    }
]

Tương tự cho các token type khác. Khi đã hoàn thành tokenize function thì coi như đã xong nửa chặng đường phát triển compiler.

Test thử cái nào:

const tokens = tokenize('234+90')
console.log(tokens)

Output:

$ tsc token.ts && node token.js
[ { type: 'NUM', value: '234' },
  { type: 'OP', value: '+' },
  { type: 'NUM', value: '90' },
  { type: 'EOF' } ]

Abstract Syntax Tree

Trong phần trên chúng ta đã có thể biến một chuỗi raw thành một dạng biểu diễn cao cấp hơn: một mảng tokens. Parser kế tiếp mà chúng ta sẽ viết sẽ nhận vào các tokens này và trả một dạng biểu diễn phức tạp hơn.

Ta đã có thể biến chuỗi thành một mảng tokens, ví dụ như expression bên dưới:

345+90

Hãy xử lí expression này một các thủ công (dùng não), đầu tiên ta thấy + là một addition operation, chúng ta lấy giá trị bên trái là 345 và giá trị bên phải là 90, và cộng chúng lại với nhau.

Thử với một cái khác phức tạp hơn đi:

345+90-88

Đầu tiên, chúng ta thấy có một addition operator và thực hiện cộng vào như trên, lúc này expression thành 435-88, và cứ tiếp tục với phép trừ thôi.

Tuy nhiên tất cả những điều trên đều chỉ xảy ra trong não của chúng ta, để Parser có thể hiểu, hãy biểu diễn chúng dưới dạng tree, từ:

345+90
    [+]
    /\
   /  \
  /    \
[345] [90]

345+90-88

thành:

Dạng tree như trên gọi là ASTNode - Abstract Syntax Tree: là một dạng cấu trúc dữ liệu để đại diện cho một expression khi được parse ra. ASTNode đại diện expression theo cách phân cấp.

Parse tree cho A + B * C - D

       [ * ]
        / \
       /   \
     [ + ]   [ - ]
      /\       /\
     /  \     /  \
   [A]  [B]  [C] [D]

Evaluate bắt đầu từ đáy lên đỉnh, ví dụ:

345+90-88

thành:

Khi leaf node [-] được evaluated, chúng ta có tree như sau:

           [ - ]
            /\
           /  \
         [255]  [88]

Và sau đó, khi [+] được evaluated:

[343]

Và chúng ta có kết quả của expression!

Tuy nhiên, mọi thứ không chỉ đơn giản ở đó, với các biểu thức toán học, các phép tính còn phải được thực hiện theo thứ tự:

BODMAS

B → Bracket
O → Of
D → Division
M → Multiplication
A → Addition
S → Subtraction

Vì vậy với expression này:

345-90+88

        [ + ]
          /\
         /  \
        /    \
      [ - ] [ 88 ]
       /\       
      /  \        
     /    \        
 [ 345 ] [ 90 ]

Chúng sẽ bắt đầu evaluate từ bên phải qua trái:

         [ + ]
          /\
         /  \
        /    \
      [ - ] [ 88 ]
       /\       
      /  \        
     /    \        
 [ 345 ] [ 90 ]
 
          |
          |
          v
          
        [ + ]
          /\
         /  \
        /    \
    [ 255 ] [ 88 ]
    
            |
            |
            v
            
        [ 343 ]
        
345-90+88 = 255+88 = 343

Như này vẫn chưa đúng vì + phải được thực hiện trước - (theo BODMAS), nên ta phải chạy 90+88 trước:

345-90+88 = 345-178 = 167

Nên ASTNode phải đổi lại như này mới đúng:

        [ - ]
          /\
         /  \
        /    \
    [ 345 ]  [ + ] 
              /\       
             /  \        
            /    \        
        [ 88 ] [ 90 ]
        
            |
            |
            v
            
        [ - ]
          /\
         /  \
        /    \
    [ 345 ] [ 178 ] 
    
            |
            |
            v
        [ 167 ]

(AST được các programming language compilers sử dụng sẽ phức tạp hơn nhiều)

Recursive Descent Parsing

Recursive Descent Parser là một giải thuật Parsing được sử dụng khá phổ biển, nó bắt đầu từ expression trên cùng hoặc ngoài cùng và và hoạt động theo cách của nó xuống các sub-expressions lồng nhau trước khi cuối cùng đến các leaf node của ASTNode.

Khi dùng RDP, các expression rule chuyển thành các functíon. Tuân theo BODMAS rule, ta thấy rằng các operation với độ ưu tiên cao sẽ ở dưới cùng của ASTNode. Vậy khi parse đệ quy mảng tokens, ta sẽ đi sâu xuống theo thứ tự ưu tiên của rule.

Hãy thể hiện rule bằng các closure functions:

type ASTNode {
}

type Operator = 'ADD' | 'SUB' | 'MUL' | 'DIV' |
  'LESS_THAN' | 'GREATER_THAN' | 'LESS_EQUAL'| 'GREATER_EQUAL' | 'EQUAL_EQUAL' | 'BANG_EQUAL'

function useBinary(left: ASTNode, operator: Operator, right: ASTNode): ASTNode {
}

function useLiteral(value: string): ASTNode {
}

function useGrouping(expr: ASTNode): ASTNode {
}

Expression rule (theo BODMAS rule):

expression → addition;

addition → subtraction(("+") subtraction)*;

subtraction → multiplication(("-") multiplication)*;

multiplication → "*" | primary;

primary → NUMBER | STRING | "false" | "true";

Dựa vào độ ưu tiên như trên, ta sẽ implement Parser như sau:

import { Token, tokenize } from "./Token";
import { useBinary, useLiteral, useGrouping } from './ast'

function useParser() {
  let index = 0
  let tokens: Token[] = null
  const expr = []

  function peep() {
    return tokens[index + 1]
  }

  function current() {
    return tokens[index]
  }

  function parse(str: string) {
    tokens = tokenize(str)
    while (current().type != 'EOF') {
      const ast = add()
      if (ast) {
        asts.push(ast)
      }
    }
    return asts
  }

  function add() {
    const left = sub()
    if (current().value === '+') {
      index++
      return useBinary(left, 'ADD', sub())
    }
    return left
  }

  function sub() {
    const left = mul()
    if (current().value === '-') {
      index++
      return useBinary(left, 'SUB', mul())
    }
    return left
  }

  function mul(): ASTNode {
    const left = all()
    if (current().value === '*') {
      index++
      return useBinary(left, 'MUL', all())
    }
    return left
  }

  function all(): ASTNode {
    const left = primary()
    switch (current().value) {
      case '>=':
        index++
        return useBinary(left, 'GREATER_EQUAL', add())
      case '<=':
        index++
        return useBinary(left, 'LESS_EQUAL', add())
      case '==':
        index++
        return useBinary(left, 'EQUAL_EQUAL', add())
      case '>':
        index++
        return useBinary(left, 'GREATER_EQUAL', add())
      case '<':
        index++
        return useBinary(left, 'LESS_THAN', add())
      case '!=':
        index++
        return useBinary(left, 'BANG_EQUAL', add())
      default:
        break
    }
    return left
  }

  function primary(): ASTNode {
    const curr = current()
    index++
    if (curr.type === 'NUM')
      return useLiteral(curr.value)
    if (curr.type === 'LPAREN') {
      const expr = add()
      index++
      return useGrouping(expr)
    }
  }

  return {
    parse
  }
}

Parser ở trên sẽ tuân theo luật ưu tiên, khi add function được gọi, bên trong add function thì operation có độ ưu tiên thấp hơn là sub() được gọi, giá trị trả về được lưu trong biến left, nếu giá trị hiện tại là phép +, một Binary object mới được tạo…

Nên với expression này:

56 - 89 * 78

        [-]
        /\
       /  \
    [*]   [56]
    /\
   /  \
[89] [78]

ASTNode như bên dưới sẽ được tạo ra:

Binary {
    type: '-',
    left: 56,
    right: Binary {
        type: '*',
        left: 89,
        right: 78
    }
}

78 * 89 - 56

Binary {
    type: '-',
    left: 78,
    right: Binary {
        type: '*',
        left: 89,
        right: 56
    }
}

Evaluating

Chúng ta đã tạo ra được ASTNode ở phần trên, giờ thì tới phần evaluate ASTNode, dùng Visitor Pattern.

Visitor Pattern giúp ta phân chia giải thuật từ một nhóm các object implement giải thuật trong một closure function.

Với mỗi ASTNode closure, ta sẽ trả về một hàm evaluate, trong hàm evaluate ta sẽ gọi giải thuật tương ứng cho việc evaluate trên ASTNode đó:

interface ASTNode {
  evaluate: () => number | boolean
}

type Operator = 'ADD' | 'SUB' | 'MUL' | 'DIV' |
  'LESS_THAN' | 'GREATER_THAN' | 'LESS_EQUAL'| 'GREATER_EQUAL' | 'EQUAL_EQUAL' | 'BANG_EQUAL'

function useBinary(left: ASTNode, operator: Operator, right: ASTNode): ASTNode {
  function evaluate(): number | boolean {
    switch (operator) {
      case 'ADD':
        return left.evaluate() + right.evaluate()
      case 'SUB':
        return left.evaluate() - right.evaluate()
      case 'MUL':
        return left.evaluate() * right.evaluate()
      case 'DIV':
        return left.evaluate() / right.evaluate()
      case 'LESS_THAN':
        return left.evaluate() < right.evaluate()
      case 'GREATER_THAN':
        return left.evaluate() > right.evaluate()
      case 'LESS_EQUAL':
        return left.evaluate() <= right.evaluate()
      case 'GREATER_EQUAL':
        return left.evaluate() >= right.evaluate()
      case 'EQUAL_EQUAL':
        return left.evaluate() == right.evaluate()
      case 'BANG_EQUAL':
        return left.evaluate() != right.evaluate()
    }
  }
  return { evaluate }
}

function useLiteral(value: string): ASTNode {
  function evaluate() {
    return Number(value)
  }
  return { evaluate }
}

function useGrouping(expr: ASTNode): ASTNode {
  function evaluate() {
    return expr.evaluate()
  }
  return { evaluate }
}

Cuối cùng hãy tạo hàm Evaluator:

function evaluate(asts: ASTNode[]) {
  console.log('RESULT:')
  for (const ast of asts) {
    console.log(ast.evaluate())
  }
}

Hàm này nhận vào các AST được tạo ra bởi Parser, sau đó loop trên array các AST Node và evaluates từng Node một.

Xem Source Code tại đây

[To be continued]