Write a "mini-compiler" in TypeScript

In programming languages, we are often familiar with the concepts of statement and expression. Statements perform an action/calculation, while expressions, when evaluated by the compiler, return a value of one of the following types:

String
Number
Boolean (true or false)
Object

In more detail, a statement is an instruction that can be executed, such as:

while
for loop
Variable assignment
Variable declaration
if else

Expressions need to be evaluated by the compiler to produce a value:

1 + 4

The expression above, when evaluated, will return the value 5:

2 < 4

And the expression above will return the value true.

So, in summary, an expression is a combination of multiple values, variables, operators, and function calls.

Statements use the value returned by expressions to perform an action or to determine a specific action that needs to be performed in that case (if / else).

Let’s take a look at the basic structure of an if statement:

if (cond expression) {
    // ...
    // body
}

The body of the if statement will be executed if the cond expression between the parentheses returns the value true.

A single value is an expression:

1
23
445
'hello'
true

These are called primary expressions. When evaluated, they will return their own value. Expressions appear on the right side of an assignment.

b = 78 * 56
a = 98 * 67 + 454 - 909

As above, these are assignments. Assignments are statements because they do not return a value. Running the above assignments in the compiler will return:

>> b = 78 * 56
>> a = 98 * 67 + 454 - 909

-> Nothing, but when we print the variables a and b:

>> b = 78 * 56
>> a = 98 * 67 + 454 - 909
>> b
4368
>> a
6111

The values of these variables are printed because they are primary expressions. The assignments above are not printed because they are statements and are only executed without being evaluated.

Some things are executed to perform an action, while others are evaluated to return an answer (a value).

Now that we understand expressions, we will try to write an evaluator program using TypeScript - this evaluator will parse and evaluate the expressions passed in.

To make it easier to visualize, the evaluator program we want to write will have output like this:

const str = `
    5+9
    3 + 3
    2 + 2 + 2;
    22*9 - 2*90
    66>=90
    90>1
    88==7
    3*250*360
    (45*89)+90
    4-5+6
    4-(5+6)
`
const asts = useParser().parse(str)
evaluate(asts)

And after running the above commands, the result returned is as follows:

$ node .
======================== RESULTS ========================
14
6
6
-3762
false
true
false
270000
4095
-7
-7

Getting Started…

First, we need to initialize a Node.js project with npm:

$ mkdir expr_parser
$ cd expr_parser
$ npm init -y

Install the TypeScript compiler:

$ npm install typescript -g

Scanning and Tokenizing

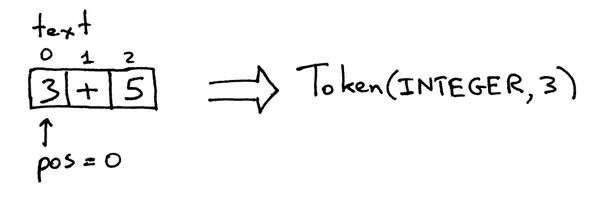
The first thing to do is to tokenize the expressions. Tokenizing means breaking down the expression into several small, separate parts.

For example:

2 + 45 - 90

The above expression can be broken down into tokens:

[
    {
        value: '2',
        type: Number
    },
    {
        value: '+',
        type: AddOp
    },
    {
        value: '45',
        type: Number
    },
    {
        value: '-',
        type: SubOp
    },
    {
        value: '90',
        type: Number
    }
]

In detail, tokenizing breaks down the components to share with the Parser what each unit represents. In the expression 2 + 45 - 90, we have 5 units or tokens:

+---+ +---+ +----+ +---+ +----+
| 2 | | + | | 45 | | - | | 90 |
+---+ +---+ +----+ +---+ +----+

In the array above, each token has a value and type. The first element in the array is a Number and the second element is an Operator +, type AddOp…

If we have an expression like this:

90 * (78 - 65) / 90

After tokenizing:

+----+ +---+ +---+ +----+ +---+ +----+ +---+ +---+ +----+
| 90 | | * | | ( | | 78 | | - | | 65 | | ) | | / | | 90 |
+----+ +---+ +---+ +----+ +---+ +----+ +---+ +---+ +----+

Represented in an array will be:

[
    {
        value: '90',
        type: Number
    },
    {
        value: '*',
        type: MulOp
    },
    {
        value: '(',
        type: LParen
    },
    {
        value: '78',
        type: Number
    },
    {
        value: '-',
        type: SubOp
    },
    {
        value: '65',
        type: Number
    },
    {
        value: ')',
        type: RParen
    },
    {
        value: '/',
        type: DivOp
    },
    {
        value: '90',
        type: Number
    }
]

These tokens will tell us what each unit of the expression represents, whether it is a Number, a Division Operator, or a Subtraction Operator, …

Now let’s create a tokenize function. This function will take one parameter: the string we want to tokenize, and return an array of tokens.

When parsing on a token, the tokenize function will also have to validate cases where the expression is considered invalid, for example, we have an expression 34+4.

3 will be a valid expression, 34 is too, 34+ is not.

import { isNum, isOp } from './utils' // Check if the string is a number / is an operator

type TokenType = 'NUM' | 'LPAREN' | 'RPAREN' | 'OP' | 'EOL' | 'EOF'

interface Token {
  type: TokenType,
  value?: string
}

function tokenize(str: string): Token[] {
  const tokens: Token[] = []

  str = str.trim()
  let s = ''
  for (let index = 0; index < str.length; index++) {
    s += str[index]
    const peek = str[index + 1]

    if (isNum(s.trim()) && !isNum(peek)) {
      tokens.push({
        type: 'NUM',
        value: s.trim()
      })
      s = ''
    }

    if (s.trim() == '(' || s.trim() == ')') {
      s.trim() == '(' ?
        tokens.push({ type: 'LPAREN' }) :
        tokens.push({ type: 'RPAREN' })
      s = ''
    }

    if (isOp(s.trim()) && !isOp(peek)) {
      tokens.push({ type: 'OP', value: s.trim() })
      s = ''
    }

    if (s == ';' || s == '\n') {
      tokens.push({ type: 'EOL' })
      s = ''
    }

    if (index == (str.length - 1)) {
      tokens.push({ type: 'EOF' })
      s = ''
    }
  }

  return tokens
}

In the tokenize function, we first trim the string to remove excess whitespace, then we loop through the elements in the string using a for loop.

Initially, we will only set the following tokens:

Numbers
Operators
Left Paren ( and Right Paren )

We concatenate each value of the current for loop index to a variable s. peak is a variable to store the value at for loop index + 1. When looping, if both s and peak are numbers, then we cannot create a number token yet because the substring of this number has not ended. Otherwise, we will create a token type Num and put it into the tokens array.

Example:

345+90

In the first loop, the variable s will have the value 3. At this time, we cannot create a token because peek has the value 4, which is still a number. Similarly, for the next loop, s = 34 and peek = 5, still not. In the third loop, s = 345 and the Number Token will be created because peek is now +, not a number. Push the number 345 into the tokens array. The tokens array at this time:

[
    {
        type: 'NUM',
        value: '345'
    }
]

Similarly for other token types. When the tokenize function is complete, it’s like we’ve finished half the journey of developing a compiler.

Let’s test it out:

const tokens = tokenize('234+90')
console.log(tokens)

Output:

$ tsc token.ts && node token.js
[ { type: 'NUM', value: '234' },
  { type: 'OP', value: '+' },
  { type: 'NUM', value: '90' },
  { type: 'EOF' } ]

Abstract Syntax Tree

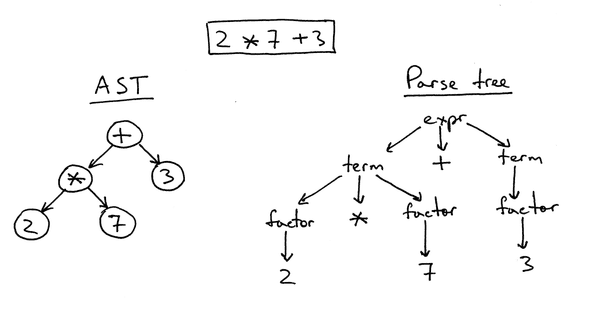
In the previous section, we were able to transform a raw string into a higher-level representation: an array of tokens. The next parser we will write will take these tokens and return a more complex representation.

We can now turn a string into an array of tokens, for example, the expression below:

345+90

Let’s handle this expression manually (using our brains). First, we see + is an addition operation. We take the value on the left, which is 345, and the value on the right, which is 90, and add them together.

Let’s try with a more complex one:

345+90-88

First, we see an addition operator and perform the addition as above. At this time, the expression becomes 435-88, and we continue with the subtraction.

However, all of the above only happens in our brains. To make the Parser understand, let’s represent them as a tree, from:

345+90
    [+]
    /\
   /  \
  /    \
[345] [90]

345+90-88

to:

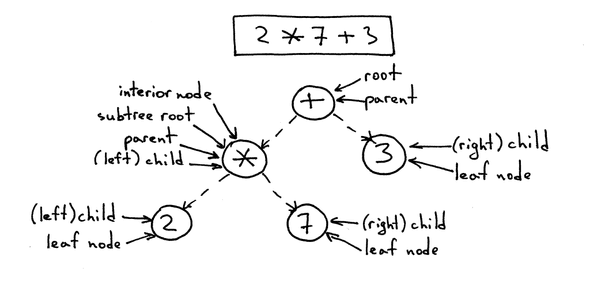
The tree form above is called ASTNode - Abstract Syntax Tree: a data structure to represent an expression when parsed. ASTNode represents the expression in a hierarchical way.

Parse tree for A + B * C - D

       [ * ]
        / \
       /   \
     [ + ]   [ - ]
      /\       /\
     /  \     /  \
   [A]  [B]  [C] [D]

Evaluation starts from the bottom up, for example:

345+90-88

becomes:

When the leaf node [-] is evaluated, we have the following tree:

           [ - ]
            /\
           /  \
         [255]  [88]

And then, when [+] is evaluated:

[343]

And we have the result of the expression!

However, things are not that simple. With mathematical expressions, calculations must also be performed in order:

BODMAS

B → Bracket
O → Of
D → Division
M → Multiplication
A → Addition
S → Subtraction

So with this expression:

345-90+88

        [ + ]
          /\
         /  \
        /    \
      [ - ] [ 88 ]
       /\       
      /  \        
     /    \        
 [ 345 ] [ 90 ]

It will start evaluating from right to left:

         [ + ]
          /\
         /  \
        /    \
      [ - ] [ 88 ]
       /\       
      /  \        
     /    \        
 [ 345 ] [ 90 ]
 
          |
          |
          v
          
        [ + ]
          /\
         /  \
        /    \
    [ 255 ] [ 88 ]
    
            |
            |
            v
            
        [ 343 ]
        
345-90+88 = 255+88 = 343

This is still not correct because + must be performed before - (according to BODMAS), so we must run 90+88 first:

345-90+88 = 345-178 = 167

So the ASTNode must be changed like this to be correct:

        [ - ]
          /\
         /  \
        /    \
    [ 345 ]  [ + ] 
              /\       
             /  \        
            /    \        
        [ 88 ] [ 90 ]
        
            |
            |
            v
            
        [ - ]
          /\
         /  \
        /    \
    [ 345 ] [ 178 ] 
    
            |
            |
            v
        [ 167 ]

(ASTs used by programming language compilers are much more complex)

Recursive Descent Parsing

Recursive Descent Parser is a popular parsing algorithm. It starts from the top or outermost expression and works its way down to nested sub-expressions before finally reaching the leaf nodes of the ASTNode.

When using RDP, expression rules translate into functions. Following the BODMAS rule, we see that operations with high precedence are at the bottom of the ASTNode. So when recursively parsing the array of tokens, we will go deeper according to the priority of the rule.

Let’s represent the rule with closure functions:

type ASTNode {
}

type Operator = 'ADD' | 'SUB' | 'MUL' | 'DIV' |
  'LESS_THAN' | 'GREATER_THAN' | 'LESS_EQUAL'| 'GREATER_EQUAL' | 'EQUAL_EQUAL' | 'BANG_EQUAL'

function useBinary(left: ASTNode, operator: Operator, right: ASTNode): ASTNode {
}

function useLiteral(value: string): ASTNode {
}

function useGrouping(expr: ASTNode): ASTNode {
}

Expression rule (according to BODMAS rule):

expression → addition;

addition → subtraction(("+") subtraction)*;

subtraction → multiplication(("-") multiplication)*;

multiplication → "*" | primary;

primary → NUMBER | STRING | "false" | "true";

Based on the priority above, we will implement the Parser as follows:

import { Token, tokenize } from "./Token";
import { useBinary, useLiteral, useGrouping } from './ast'

function useParser() {
  let index = 0
  let tokens: Token[] = null
  const expr = []

  function peep() {
    return tokens[index + 1]
  }

  function current() {
    return tokens[index]
  }

  function parse(str: string) {
    tokens = tokenize(str)
    while (current().type != 'EOF') {
      const ast = add()
      if (ast) {
        asts.push(ast)
      }
    }
    return asts
  }

  function add() {
    const left = sub()
    if (current().value === '+') {
      index++
      return useBinary(left, 'ADD', sub())
    }
    return left
  }

  function sub() {
    const left = mul()
    if (current().value === '-') {
      index++
      return useBinary(left, 'SUB', mul())
    }
    return left
  }

  function mul(): ASTNode {
    const left = all()
    if (current().value === '*') {
      index++
      return useBinary(left, 'MUL', all())
    }
    return left
  }

  function all(): ASTNode {
    const left = primary()
    switch (current().value) {
      case '>=':
        index++
        return useBinary(left, 'GREATER_EQUAL', add())
      case '<=':
        index++
        return useBinary(left, 'LESS_EQUAL', add())
      case '==':
        index++
        return useBinary(left, 'EQUAL_EQUAL', add())
      case '>':
        index++
        return useBinary(left, 'GREATER_EQUAL', add())
      case '<':
        index++
        return useBinary(left, 'LESS_THAN', add())
      case '!=':
        index++
        return useBinary(left, 'BANG_EQUAL', add())
      default:
        break
    }
    return left
  }

  function primary(): ASTNode {
    const curr = current()
    index++
    if (curr.type === 'NUM')
      return useLiteral(curr.value)
    if (curr.type === 'LPAREN') {
      const expr = add()
      index++
      return useGrouping(expr)
    }
  }

  return {
    parse
  }
}

The parser above will follow the priority rules. When the add function is called, inside the add function, the operation with lower priority, sub(), is called. The return value is stored in the left variable. If the current value is the + operator, a new Binary object is created…

So with this expression:

56 - 89 * 78

        [-]
        /\
       /  \
    [*]   [56]
    /\
   /  \
[89] [78]

The ASTNode below will be created:

Binary {
    type: '-',
    left: 56,
    right: Binary {
        type: '*',
        left: 89,
        right: 78
    }
}

78 * 89 - 56

Binary {
    type: '-',
    left: 78,
    right: Binary {
        type: '*',
        left: 89,
        right: 56
    }
}

Evaluating

We have created the ASTNode in the previous section, now it’s time to evaluate the ASTNode, using the Visitor Pattern.

The Visitor Pattern helps us separate the algorithm from a group of objects that implement the algorithm in a closure function.

For each ASTNode closure, we will return an evaluate function. In the evaluate function, we will call the corresponding algorithm for evaluating that ASTNode:

interface ASTNode {
  evaluate: () => number | boolean
}

type Operator = 'ADD' | 'SUB' | 'MUL' | 'DIV' |
  'LESS_THAN' | 'GREATER_THAN' | 'LESS_EQUAL'| 'GREATER_EQUAL' | 'EQUAL_EQUAL' | 'BANG_EQUAL'

function useBinary(left: ASTNode, operator: Operator, right: ASTNode): ASTNode {
  function evaluate(): number | boolean {
    switch (operator) {
      case 'ADD':
        return left.evaluate() + right.evaluate()
      case 'SUB':
        return left.evaluate() - right.evaluate()
      case 'MUL':
        return left.evaluate() * right.evaluate()
      case 'DIV':
        return left.evaluate() / right.evaluate()
      case 'LESS_THAN':
        return left.evaluate() < right.evaluate()
      case 'GREATER_THAN':
        return left.evaluate() > right.evaluate()
      case 'LESS_EQUAL':
        return left.evaluate() <= right.evaluate()
      case 'GREATER_EQUAL':
        return left.evaluate() >= right.evaluate()
      case 'EQUAL_EQUAL':
        return left.evaluate() == right.evaluate()
      case 'BANG_EQUAL':
        return left.evaluate() != right.evaluate()
    }
  }
  return { evaluate }
}

function useLiteral(value: string): ASTNode {
  function evaluate() {
    return Number(value)
  }
  return { evaluate }
}

function useGrouping(expr: ASTNode): ASTNode {
  function evaluate() {
    return expr.evaluate()
  }
  return { evaluate }
}

Finally, let’s create the Evaluator function:

function evaluate(asts: ASTNode[]) {
  console.log('RESULT:')
  for (const ast of asts) {
    console.log(ast.evaluate())
  }
}

This function takes the ASTs created by the Parser, then loops through the array of AST Nodes and evaluates each Node.

See the Source Code here.

[To be continued]

Getting Started…

Scanning and Tokenizing

Abstract Syntax Tree

Recursive Descent Parsing

Evaluating

Subscribe to my newsletter